a-b剪枝技术是什么：

a-b剪枝算法是一个搜索算法旨在减少在其搜索树中，被极大极小算法评估的节点数。这是一个常用人机游戏对抗的搜索算法。它的基本思想是根据上一层已经得到的当前最优结果，决定目前的搜索是否要继续下去。

a-b剪枝算法是对Minimax方法的优化，它们产生的结果是完全相同的，只不过运行效率不一样。

这种方法的前提假设与Minimax也是一样的：

   1）双方都按自己认为的最佳着法行棋。

   2）对给定的盘面用一个分值来评估，这个评估值永远是从一方（搜索程序）来评价的，红方有利时给一个正数，黑方有利时给一个负数。（如果红方有利时返回正数，当轮到黑方走棋时，评估值又转换到黑方的观点，如果认为黑方有利，也返回正数，这种评估方法都不适合于常规的算法描述）。

   3）从我们的搜索程序（通常把它称为Max）看来，分值大的数表示对己方有利，而对于对方Min来说，它会选择分值小的着法。

a-b剪枝技术只能用递归来实现。这个思想是在搜索中传递两个值，第一个值是a，即搜索到的最好值，任何比它更小的值就没用了，因为策略就是知道a的值，任何小于或等于a的值的合理着法都不会对整个局面的获胜率有更高的提高。

   第二个值是b，即对于对手来说最坏的值。这是对手所能承受的最坏的结果，因为我们知道在对手看来，他总是会找到一个对策不比b更坏的。如果搜索过程中返回b或比b更好的值，那就够好的了，走棋的一方就没有机会使用这种策略。

在搜索着法时，每个搜索过的着法都返回跟a和b有关的值，它们之间的关系非常重要，或许意味着搜索可以停止并返回。

如果某个着法的结果小于或等于a，那么它就是很差的着法，因此可以抛弃。因为我前面说过，在这个策略中，局面对走棋的一方来说是以a为评价的。

如果某个着法的结果大于或等于b ，那么整个节点就作废了，因为对手不希望走到这个局面，而它有别的着法可以避免到达这个局面。因此如果我们找到的评价大于或等于b ，就证明了这个结点是不会发生的，因此剩下的合理着法没有必要再搜索。

   如果某个着法的结果大于a但小于b，那么这个着法就是走棋一方可以考虑走的，除非以后有所变化。因此a会不断增加以反映新的情况。有时候可能一个合理着法也不超过a ，这在实战中是经常发生的，此时这种局面是不予考虑的，为了避免这样的局面，我们必须在博弈树的上一个层局面中选择另外一个着法。

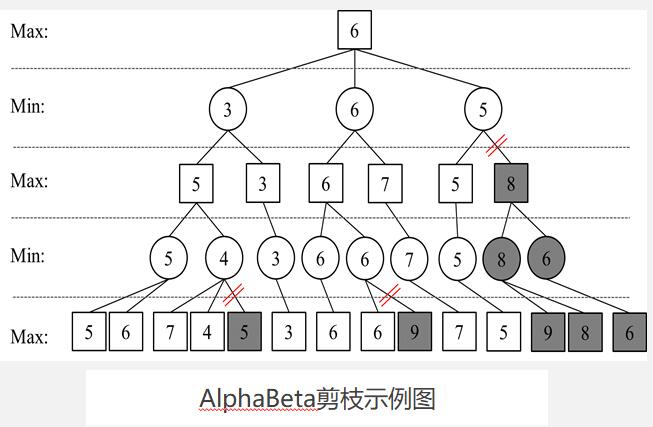
下图中第四层的4的b值为4比其父节点的a值5要小，所以将其剩余的枝剪去。